Anya Chung
is a graphic designer and brand strategist. I’m currently at Deloitte Digital, where I work on systems design, UX, and strategy. My design practice is inspired by the logic of systems, the nuances of brand identities, character design, humor, and flowers.
About︎︎︎ Email︎︎︎ LinkedIn︎︎︎
Los Angeles
Anya Chung
About︎︎︎
Email︎︎︎
LinkedIn︎︎︎
Index
LangChain
ASTRO
Asteria
MASH
Hilbert’s Axioms
Yuna Headphones
Call Flowers
Bits and bobs
Los Angeles
Hilbert’s Axioms
Hilbert’s axioms consist of three tautologies — logical sentences that always return as true, no matter what the truth values of the letters are.
Hilbert’s axioms are:
A → (B → A)
(A → (B → C)) → ((A → B) → (A → C))
(¬A → ¬B) → (B → A)
Hilbert’s axioms are:
A → (B → A)
(A → (B → C)) → ((A → B) → (A → C))
(¬A → ¬B) → (B → A)
These axioms, along with the rule of Modus Ponens, construct Hilbert’s proof system for classical logic.
Letters can either be true or false — here, blue dots represent “true” letters and orange diamonds represent “false” ones. This visualization takes every possible combination for each axiom — a total of sixteen different possibilities — and traces their paths to truth.
Letters can either be true or false — here, blue dots represent “true” letters and orange diamonds represent “false” ones. This visualization takes every possible combination for each axiom — a total of sixteen different possibilities — and traces their paths to truth.
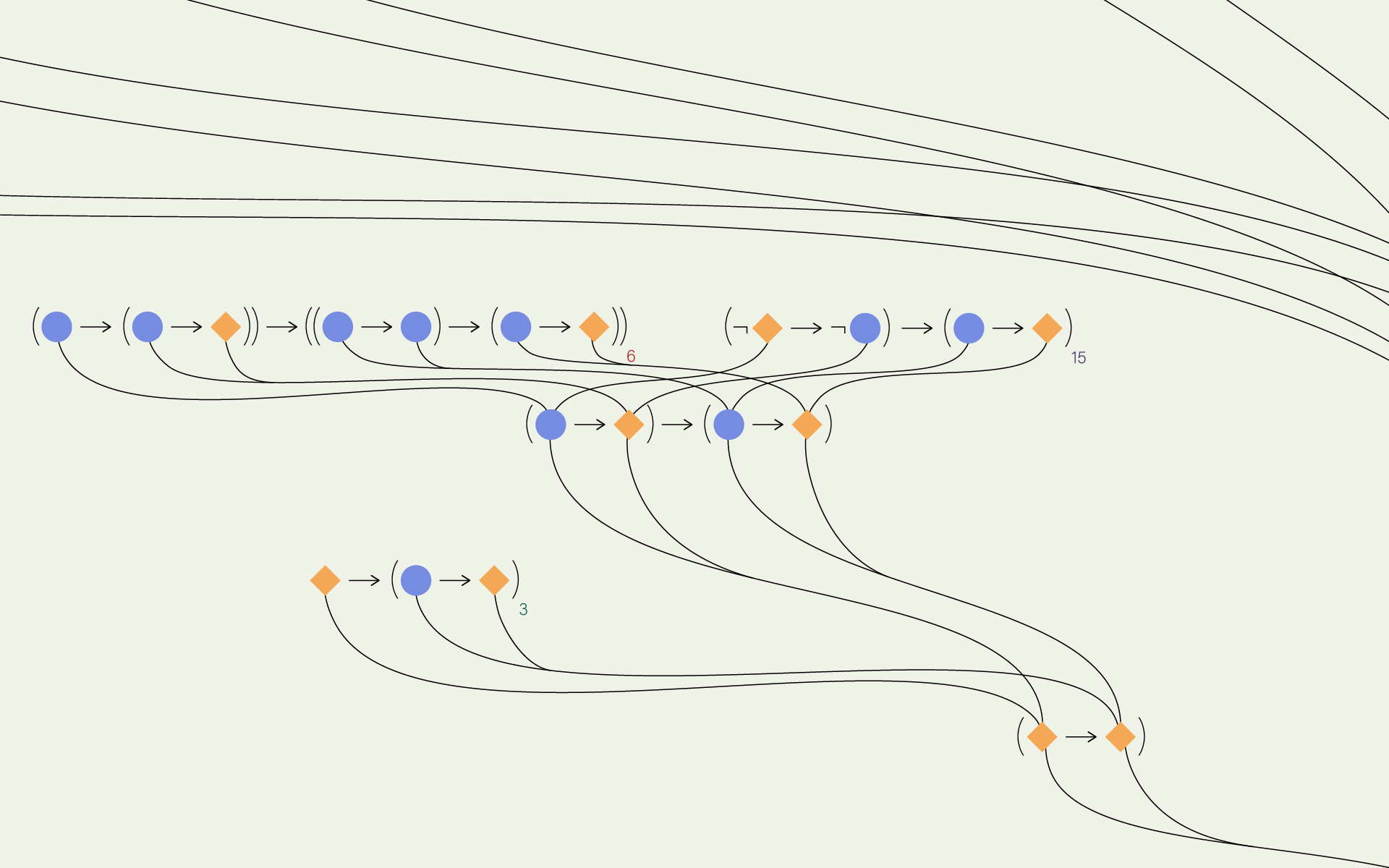
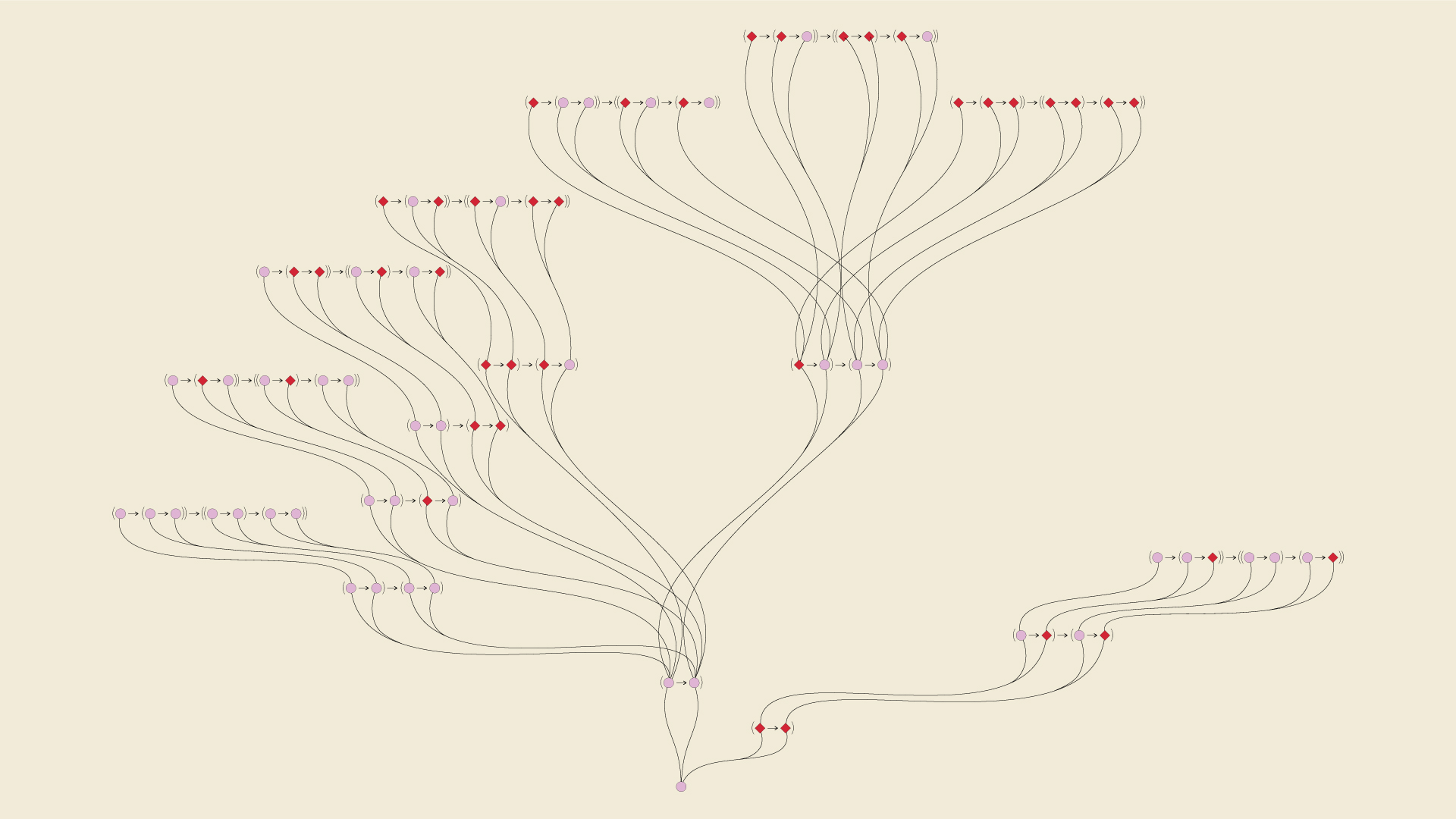
Hilbert's Second Axiom System
